Liquid Droplets

Introduction

Droplets are interacting Lagrangian spheres that can access continuous positions across the fluid lattice. Droplets are typically used to model two-fluid droplet dispersion, but also have application to blending density-stratified miscible fluids

Each droplet has a rigid core that interacts elastically with the rigid cores of other dispersed-phase particles. The purpose of the hard sphere interactions is to ensure that the initial dispersed phase volume remains incompressible prior to droplet breakup/dispersion.

Surrounding each rigid core is a fully penetrable concentric exterior shell which increases the apparent volume of the particle. The purpose of the shell is to allow the dispersed phase volume fraction to overcome the 0.62 limit on volume fraction presented by random sphere packing. That is, by accounting for the interstitial region between a random pack of rigid spheres, the dispersed phase volume fraction reconstructed from the cherry-pit particles can realize values close to 1.0.

Droplets enter the system within as monodisperse particles located within the children geometry of the droplet parent. The droplet volume fraction and size distribution can inform the local fluid viscosity via a user-defined rheology. Droplet positions and velocities evolve according to Newton’s Second Law using a Verlet algorithm advanced at the simulation time step. The forces included in the velocity update are defined by the user.

Upon entering the simulation domain, each droplet is assigned an ID, a birth timestamp, a diameter, and an origin ID. The birth timestamp identifies the time step at which each droplet enters the system. This value is particularly useful in predicting droplet residence time distributions and droplet mean age. The origin ID describes where a droplet entered the system. This value is useful in predicting how droplets from various sources blend and transfer mass to/from the fluid. It is also useful in predicting how droplets with different properties (e.g., density and diameter) are affected by fluid motion (assuming different droplet properties are assigned to the different droplet origins).

Breakup occurs on the level of individual droplet or using a parcel approach. In either approach, the daughter diameter is informed by the physical properties of the droplet and the kinematic properties of the fluid. Coalescence also occurs at the level of individual droplets or using a parcel approach. In the former, coalescence is informed by the kinematic properties of the two droplets. In the latter, changes in the parcel diameter are informed by the kinematic properties of the fluid.

Mass transfer between droplets and the surrounding fluid are discussed Droplet/Scalar Coupling. The mass transfer coefficient of each droplet is a user-defined function governed by local fluid properties. This droplet-specific mass transfer rate multiplied by the local droplet/fluid concentration difference defines the mass transfer rate between droplets and the surrounding fluid. Mass leaving/entering the droplet causes the droplet to shrink/grow in a way that conserves total species mass.

Note

Droplet image files are printed at the same frequency as slices and volumes.

Property Grid

General

Injection Option

Injection option.

Dump

TBA.

Initial Packing

This option describes where the initial volume fraction of the dispersed phase/droplets within the system.

Auto

Set number of packed droplets based on initial droplet diameter and voxelized volume at runtime. The dispersed phase volume fraction is assumed to be 1.0 and the number of initial droplets is calculated at runtime to fill the child geometry.

Custom

User-defined expression defining the number of droplets initially injected into the child geometry. This expression may be a function of the child volume, enabling the user to define a local dispersed phase volume fraction.

Initial Packing Volume Fraction

Definition

Dump Time UDF

s | Time to begin droplet addition.

No Injection

TBA.

Density

kg/m ³ | Density of the dispersed phase droplets.

Note

In addition to hard sphere droplet-droplet interactions, the trajectories of each droplet are informed by the weight, buoyancy, drag, and virtual mass forces.

Volumetric Generation

This functionality is used to dynamically generate particles across the fluid domain according to user-defined generation criteria. The generation criteria are applied on a voxel-by-voxel basis and can be a function of local fluid properties and/or system-level variables. Volumetric generation is typically used to model nucleation processes.

Enabled

Enable an injection based on local fluid conditions.

On

Volumetric generation enabled.

Interval

Time interval at which the generation criteria is tested. Shortening this interval increases the frequency at which the injection criteria is tested.

Injection Condition UDF

dimensionless and m | This UDF defines the local conditions for particle injection as part of a volumetric particle generation routine. It requires two output variables: a Boolean named inject and a floating-point variable named d.

The inject Boolean determines whether particle injection occurs in each voxel. If inject is true, d specifies the diameter of the particle added to the voxel, with the addition position randomized within the voxel. In this way, inject controls where injection occurs across the simulation domain, while d sets the local diameter of the injected particles.

The output Boolean inject is dimensionless while the output floating point value d has units of meters. Both variables are voxel-based local UDFs, calculated on a voxel-by-voxel basis using the local fluid properties.

Download Sample File: Injection Condition

Off

No volumetric generation.

Forces and Fluid Coupling

See additional forces and fluid coupling overview.

Gravity/Buoyancy Force

This force represents the net effect of gravity and buoyancy.

Virtual Mass

The virtual mass refers to the virtual increase in the effective mass of a particle moving through fluid due to the inertia of the surrounding fluid.

Lift (Saffman)

The Saffman lift force arises when a particle experiences a cross-flow induced by the rotation of the particle.

Drag Force Model

The drag force is the resistance encountered by particles as they move through the fluid medium.

Two Way Coupling

Two-way coupling describes the mutual interaction between fluid flow and particle motion.

Fluid-Particle Force UDF

This UDF defines custom vectors for fluid and external forces acting on particles.

If a static body is present, the following section will launch:

Static Body Interaction

Static Body Option

This parameter specifies how each particle set interacts with each solid body family.

Bounce

The particles bounce off the solid body family.

Stick

The particles stick to the solid body family.

Pass Thru

The particles pass through the solid body family.

Breakup/Coalesce

Particle breakup and coalescence can be modeled using either discrete or parcel-based representations.

In the discrete representation, particle breakup occurs on a particle-by-particle basis and generates a new particle that is explicitly tracked in the simulation; this new particle inherits the properties of the mother particle from which it was broken off. Particle coalescence is regulated at the level of individual particle pairs by comparing the approach Reynold’s number to a critical coalescence parameter. Coalescence events reduce the number of explicitly tracked bubbles.

In the parcel-based representation, both particle breakup and coalescence are regulated implicitly by adjusting the number scale associated with each parcel. Changes in diameter are informed by the local fluid properties which, when combined with surface tension and density, define an equilibrium particle diameter. With this approach, the number of explicitly tracked particles does not change due to breakup or coalescence events. See additional breakup/coalesce overview.

Breakup Enabled

Particle breakup typically occurs on the level of individual particles and is informed by the physical properties of the particle and the kinematic properties of the fluid.

Coalesce Enabled

Coalescence typically occurs at the level of particle pairs and is informed by the kinematic properties of the two particles.

Interfacial Mass Transfer

Interfacial mass transfer is calculated on a particle-by-particle basis using the local and instantaneous fluid and particle properties. This can be represented as either a convective transfer coefficient, \(k_L\), or a particle dissolution rate. In principle, the convective transfer coefficient and the dissolution rate describe very similar physical transport processes. In practice, a convective transfer coefficient is typically applied to gas bubbles and a dissolution rate is applied to solid particles.

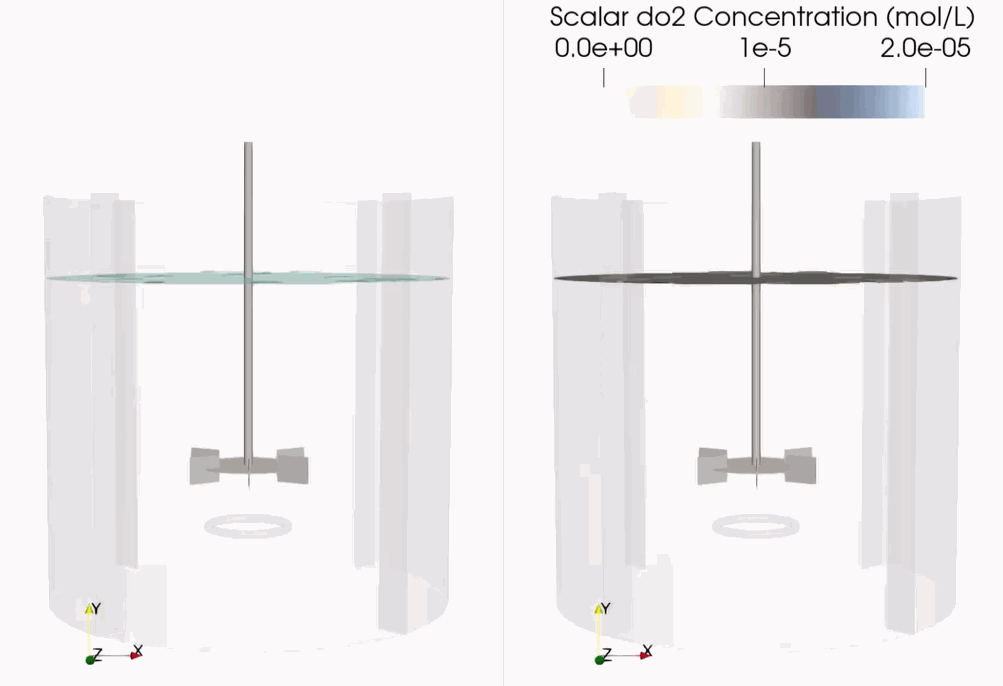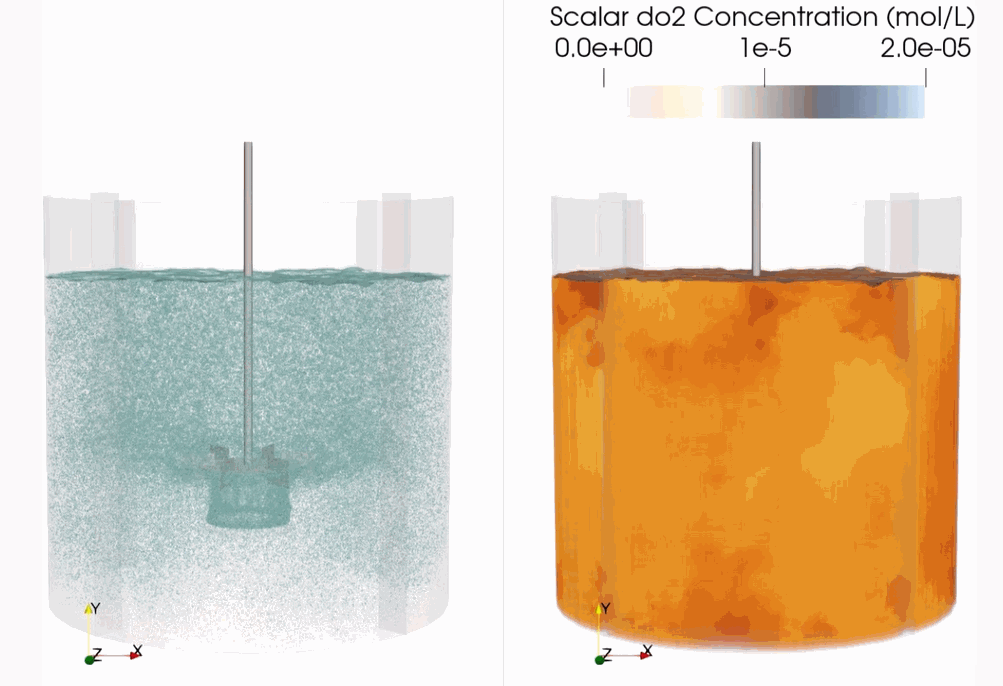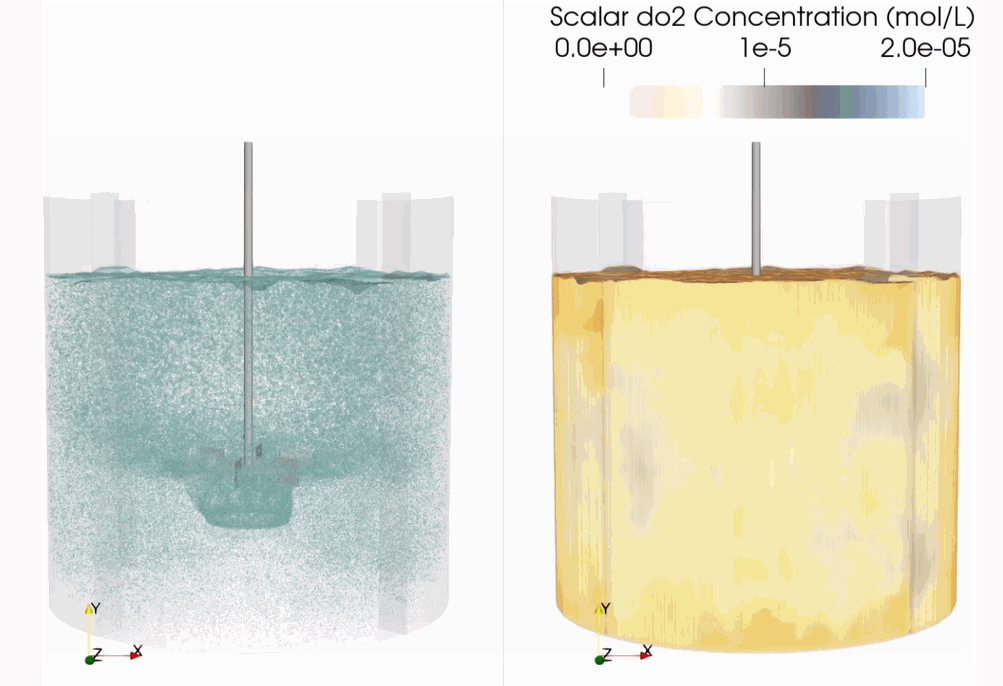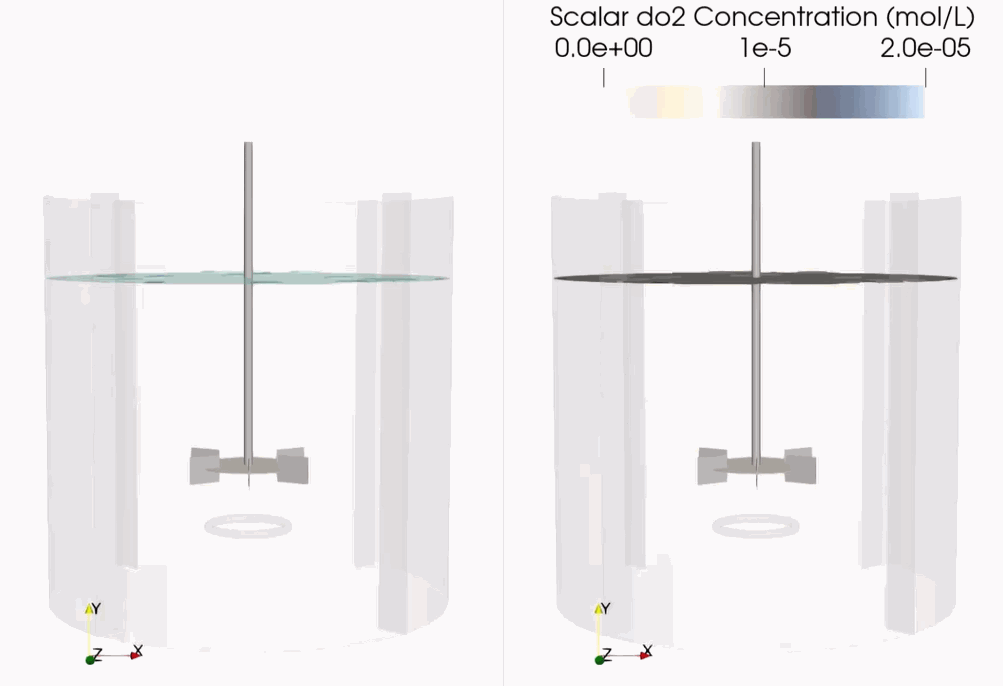
Download Sample File: Scalar Coupling

Mechanically speaking, the convective transfer coefficient describes the rate at which mass is transferred (via convection) through the fluid boundary layer surrounding the particle. This rate is often written in terms of the local fluid energy dissipation rate, fluid viscosity, and fluid diffusion coefficient; although, in many cases a constant transfer coefficient may be suitable.

Theoretically speaking, most convective mass transfer models are developed under the assumption that the fluid immediately surrounding the particle remains fully saturated throughout the transport process. The rate at which mass is transferred into the system is therefore a function of the rate at which the saturated fluid adjacent to the bubble surface can be engulfed into the fluid bulk. These transfer functions can be derived from semi-empirical boundary layer theory.

Conversely, particle dissolution rates are developed under the assumption that the dissolved species concentration is low relative to the solid phase concentration. As such, the transfer rate is often related to the system temperature and the physiochemical properties of the solid rather than to the convective properties of the fluid surrounding the solid. In many cases, the dissolution rate is set to a constant value determined empirically.

Framework

This parameter determines whether mass transfer is modeled using the convective transfer coefficient or the particle dissolution rate. These values are calculated on a particle-by-particle basis using the local and instantaneous particle and/or fluid properties.

Convection

This calculates a convective mass transfer coefficient for each particle. Input to this expression includes the local and instantaneous properties of the particle and surrounding fluid.

kL UDF

m/s | This UDF defines the convective mass transfer coefficient in the fluid surrounding a particle. One output must be defined within the UDF: a floating-point variable named kl_{Particles}, where {Particles} is the dynamic name of the particle set. This output value is used when predicting convective mass transfer processes, including mass exchange with coupled scalar fields. This is a particle-based local UDF, calculated on a particle-by-particle basis using the local particle/fluid properties.

Download Sample File: kL

Dissolution

This calculates a dissolution rate for each particle. Possible input to this expression includes the local and instantaneous properties of the particle and surrounding fluid.

Dissolution Rate UDF

\(\frac{kg}{m^2 \cdot s}\) | This UDF defines the particle dissolution rate, defined here as the rate at which mass is exchanged between the solid phase (particles) and the dissolved phase/solute (coupled scalar field). One output must be defined as within the UDF: a floating point variable named dr_{Particle Set Name}, where {Particle Set Name} is the dynamic name of the particle set parent.

This output value defines the particle-specific dissolution rate. Positive values imply dissolution (mass leaving the particle). Negative values imply precipitation or crystallization. The units on the output variable are kg/m ² /s. This is a particle-based local UDF, calculated on a particle-by-particle basis using the local particle/fluid properties.

Download Sample File: Dissolution Rate

None

No mass transfer coefficient or dissolution rate is calculated.

Droplet/Scalar Coupling

Mass transfer between a droplet and the surrounding fluid is informed by the local fluid mass transfer coefficient, the surface area of the droplet, and the species concentration difference. With the Droplet/Scalar Coupling option, users can model species exchange between the fluid and individual droplet, along with the associated changes in droplet size and composition (if multiple species are present).

Initial Volume Fraction

This value defines the fraction of the droplet initially occupied by each scalar. If multiple coupled scalar fields are present, the sum of all volume fractions must be equal to one.

Molar volume

m ³ /mol | Volume of space occupied by each mole of gas in the droplet for each species. This value defines the change in the droplet volume due to mass transfer with the surrounding fluid. A value of zero implies the mass transfer for this species involves no change in the droplet diameter. Note that the volume of ideal gas at standard temperature and pressure is 0.0224 m ³/ mol.

Coupling Model

Two methods are available for modeling mass transfer: (i) Fick’s Law and (ii) Custom.

Fick’s Law

In this approach, mass transfer is modeled as:

\[\dot{n}=k_L A \left( C_{g,i}-C_{f,i} \right)\]

where

\(\dot{n}\) is a mass flow rate between the droplet and the surrounding fluid [mol/s], \(k_L\) is the mass transfer coefficient of the fluid surrounding the droplet [m/s], \(A\) is the surface area of the droplet [m ²], \(C_g\) is the saturated concentration of species \(i\) [mol/m ³ ], and \(C_f\) is the local fluid concentration of species \(i\) [mol/m ³ ].

Note that the user must define the saturated concentration of each species.

Custom

In this approach, the user defines a custom mass transfer model for each species per the local fluid properties and the diameter/composition of each droplet. These models can follow the functional form of Fick’s law or be extended to model more complex reaction/dissolution processes.

Advanced

Initial Droplet Diameter Option

By default, the initial droplet diameter is equal to the lattice spacing. Smaller initial droplet diameters can be specified here. This value represents a ceiling on the maximum droplet diameter. Droplets with diameters larger than the lattice spacing are not recommended.

Auto

Custom

DEM Bounce Method

This options for this method defines how the particles interact with solid bodies. The video below shows the difference between the two options.

Cell

This is the default option. It is computationally faster than Triangle method. The particles interact with the boundaries of the fluid voxels. Smaller particles, can get caught on the “steps” for coarser resolutions. As the lattice resolution increase, this effect is minimized.

Triangle

In this option, the particles interact with the triangles made from the tessellation of the static body surface. This is more computationally expensive than the Cell option, but results in a more physically realistic interaction with the static body. The size of the triangles used to represent the surface is set using the edit mesh form. The corresponding mesh can be previewed using the Preview Surface Meshes tool.

Compute Nearest Neighbor Distribution

Computes the average nearest neighbor separation distance and nearest neighbor separation distance probability distribution function. See additional discussion in Theory: Nearest Neighbor Distribution.

On

Particle distribution data is computed.

Off

Particle distribution data is not computed.

Enable Movement Control

With this option, users can define a UDF that conditionally controls whether particles are moving or fixed. Particle motion can be reactivated as part of the UDF.

On

Movement control of particles is enabled. Individual particles may become fixed in space per some user-defined condition.

Movement Control UDF

none | This UDF defines if individual particles move or remain fixed in space. One of two possible boolean outputs can be defined as part of the UDF: makeFixed and makeMoving. The values assigned to each value can change over time. If the boolean makeMoving is set to true, the particle will evolve through space. Only one boolean should be true at each time step. This is a local UDF, calculated on a particle-by-particle basis using the local particle/fluid properties.

Download Sample File: Movement Contol

Off

No controlled movement of particles. Particles always have the ability to move through space.

Compute Pressure Gradient Force

When this option is active, the pressure gradient force on the particle is calculated. This force acts from regions of higher pressure toward regions of lower pressure, influencing the motion of particles immersed in the fluid.

For a small particle within a fluid, the pressure gradient force can be expressed as:​

\[F_p = - V_p \nabla P\]

where \(V_p\) is the volume of the particle and \(\nabla P\) is the pressure gradient and the location of the particle.

Off

Does not compute pressure gradient force.

On

Computes pressure gradient force.

Enable Removal UDF

Enable removal user-defined function.

Removal UDF

no units | This UDF removes particles based on particle properties or local fluid conditions. One output must defined within the UDF: a Boolean variable named remove. This output value determines if a particle is to be removed from the simulation. If set to true, the particle is removed. This is a local UDF, calculated on a particle-by-particle basis using the local particle/fluid properties.

Download Sample File: Removal

Liquid Droplets Toolbar

Context-Specific Toolbar Forms	Description
Add Geometry	The Add Geometry form adds child geometry by importing from external CAD files, extracting from external CAD assemblies, or defining internally using built-in parametric geometry.
Move	The Move form enables three-dimensional rigid body transform of object through free drag or point-to-point snapping.
Rotate	The Rotate form enables three-dimensional rotation of geometry.
Scale	The Scale form enables volumetric scaling of a geometry about a set anchor point.
Mate	The Mate form allows surface-to-surface mating and alignment.
Add Particle Injection	The Add Particle Injection adds an injection to a particle parent.
Add Particle Scalar	The Add Particle Scalar tool assigns custom properties to individual particles which move with them and can be used to model intraparticle reactions.
Add Particle Reaction	The Add Particle Reaction tool applies user-defined kinetics to each particle based on its composition and surrounding fluid properties.
Add Particle Variable	The Add Particle Variable tool defines per-particle quantities via UDFs, accessing particle properties and local fluid conditions.
Add Fill Point	The Add Fill Point selects which space will initially be 3D-filled with a liquid.
Diagnostics	The Diagnostics form reports the position, orientation, and moments of inertia associated with a static body.
Help	The Help command launches the M-Star reference documentation in your web browser.

See also Child Geometry Context Specific Toolbar.

For a full description of each selection on the Context-Specific Toolbar, see Toolbar Selections.