Discrete Element Particles¶

Introduction¶

Discrete Element Particles extend the functionality of inertial particles to include particle-particle contact mechanics. These particles are useful for performing discrete element method (DEM) simulations as well as coupled CFD-DEM simulations. Typical applications include systems with high solids concentrations such as slurries, granular flows, and particle packing problems.

Unresolved DEM Particles

DEM interactions are typically described using a Hertz contact model, although more sophisticated models are available. CFD-DEM simulations are an advanced modeling paradigm and should be used purposefully. They typically require smaller timesteps to remain numerically stable and can increase runtimes.

Like inertial particles, DEM particles can be coupled to fluid scalar fields and participate in chemical reactions. DEM particle momentum can likewise be either one- or two-way coupled to the fluid. As with both inertial and tracer particles, DEM particles can also be assigned particle variables, which can be used to investigate the system from the perspective of a moving particle (e.g., cell or crystal grain).

Because DEM particles consider pair-wise interactions, care must be taken to avoid unphysical overpacking, where the number of particles is added to a child geometry. That is, unlike non-interacting inertial and tracer particles, particle addition is limited by the system volume.

Resolved DEM Particles

Both unresolved and resolved DEM particle representations are available. Unresolved particles are small compared to the lattice spacing, and the flow field around the particle is not explicitly resolved. Instead, for unresolved particles, interactions (e.g., particle drag, lift) are modeled using empirical correlations. Resolved particles are large compared to the lattice spacing, meaning the flow field/fluid boundary layer around the particle is resolved explicitly.

For more on this topic, check out these webinars.

Adding Discrete Element Particles¶

When adding particles to a system, there are two factors to consider: (1) the number of particles entering the system, and (2) the location of the particles entering the system.

The number of particles entering the system is defined by an injection rate and an injection duration. Pay close attention to the appropriate number of particles added to the system as very large particle counts can slow performance. Various injection options are provided for defining these parameters.
The location of the particle injection is typically defined using children geometry, an injection zone, an inlet boundary condition, or a background injection:
- A child geometry injection represents the superposition of particles on the fluid field within a sub-volume of the fluid domain. Fluid flow sweeps these particles from the initial positions within the child geometry to other regions in the system. The particle properties, such as initial size distribution, composition, and injection rate, are all inherited from the parent. All children inherit the same properties.
- An injection zone allows users to define custom injection regions with local injection rates, injection size distributions, and initial particle compositions that differ from those defined on the particle parent. Particle injection zones allow for differentiated particle injection characteristics within a particle family. Children geometry can be added to the injection zone to control where localize where particles associated with the injection zone are added to the system.
- An inlet boundary condition represents the superposition of particles on the fluid field along the boundary condition surface. Boundary condition flow sweeps these particles from the initial positions along the boundary condition to other regions in the system.
- A background injection produces a uniform distribution of particles across the full fluid field. This addition, if applied at the start of a process, represents a system with an initially well-dispersed ensemble of particles.

When using a child geometry injection, users have three options for adding geometry to the particle parent: (1) via the Add Geometry form, which opens automatically when a new particle parent is created; (2) by importing geometry through the Assembly Explorer; or (3) by importing geometry from a spreadsheet. See the Geometry page for more details.

For an already-existing parent component, you can add children via the Add Geometry command found on the Context Specific Toolbar. Children geometry can also be extracted from an assembly file.

Discrete element particles can also enter the system through Eularian conversion and volumetric generation via a user-defined function. Eularian conversion is used to model fluid-to-fluid conversion processes, as realized during jet breakup, air entrainment, and two-fluid dispersion processes. Volumetric generation is used to model particle nucleation, particle crystallization, and so forth.

Note

Use caution when adding more than a billion particles. System memory limits the total number of particles that can be tracked. On a single workstation, this limit is 50–100 million particles. On a GPU cluster, this limit is about 1 billion particles.

Warning

The number of DEM particles added to a child volume cannot exceed the maximum solids packing fraction within the child volume. For most systems, this maximum solid packing fraction is around 60–70%. If the requested particle injection or feed rate exceeds this maximum value, the code will not be able to fit all the requested particles into the injection volume.

For dump-type injections, overpacking conditions will cause the code to exit with an error and report the maximum particle overlap. High initial overlap values, which imply particle overpacking, can be avoided by either (i) increasing the size of the injection volume or (ii) reducing the number of particles added to the injection geometry.

For feed-type injections, overpacking conditions will cause the code to produce a warning when the realized injection rate does not achieve the set injection rate. The difference between the realized particle addition and the target particle addition will be reported. Per the engineering judgment of the user, small differences between the set and realized particle injection may be acceptable. To reduce this difference, however, users can either (i) increase the size of the injection volume, (ii) reduce the particle feed rate into the injection geometry, or (iii) increase the velocity of the fluid transporting particles away from the injection geometry.

Property Grid¶

`General`¶

This option controls the type of particle injections and the density of the particles which will be added to the system. Consider both the number and the location of the particles when adding particles to the system. The injection options are listed below and discussed in greater detail in the injection options overview.

Injection Option

This setting contains the different selections for introducing particles into a system. The number of particles added to the system is determined by an injection rate and an injection duration.

Dump: A single impulse addition of particles into the injection geometry. The dump defines the total number of particles added to the system at a single user-defined time.
Feed: A continuous feed of particles into the injection geometry at a user-defined number flow rate over a user-defined period. The feed rate can vary per user-defined expression.
Volume Feed: A continuous feed of particles into the injection geometry at a user-defined volume flow rate for a user-defined period.
Initial Mass Fraction: A single impulse addition of particles into the injection geometry at a user-defined fraction of the mass of the injection geometry.
Initial Volume Fraction: A single impulse addition of particles into the injection geometry at a user-defined fraction of the volume of the injection geometry.
Total Mass: A single impulse addition of particles into the injection geometry at a user-defined total mass.
No Injection: The particle feed rate is not directly controlled by the user. Particles are dynamically generated across the system via free-surface Eularian-Lagrangian conversion, immiscible two fluid Eularian-Lagrangian conversion, or volumetric particle generation.

Density: kg/m ³ | The density of the particles added via this injection.

`Volumetric Generation`¶

This functionality is used to dynamically generate particles across the fluid domain according to user-defined generation criteria. The generation criteria are applied on a voxel-by-voxel basis and can be a function of local fluid properties and/or system-level variables. Volumetric generation is typically used to model nucleation processes.

Enabled

This enables volumetric generation based on local fluid conditions.

On

Volumetric generation enabled.

Interval

The time interval at which the generation criteria are tested. Shortening this interval increases the frequency at which the injection criteria are tested.

Injection Condition UDF

dimensionless and m | This UDF defines the local conditions for particle injection as part of a volumetric particle generation routine. It requires two output variables: a Boolean named inject and a floating-point variable named d.

The inject Boolean determines whether particle injection occurs in each voxel. If inject is true, d specifies the diameter of the particle added to the voxel, with the addition position randomized within the voxel. In this way, inject controls where injection occurs across the simulation domain, while d sets the local diameter of the injected particles.

The output Boolean inject is dimensionless while the output floating point value d has units of meters. Both variables are voxel-based local UDFs, calculated on a voxel-by-voxel basis using the local fluid properties.

Download Sample File: Injection Condition

Off

No volumetric generation.

`Initial Size Distribution`¶

Particle sizes are described by the diameter. The specified size distribution of particles can be previewed by clicking on the plot distribution icon in the property grid. See additional size distribution overview.

Distribution Type

The following are the options for initial particle size distribution.

Single: The diameter of the particles is set by the user and assigned to all particles. This condition represents the addition of monodispersed particles.
Uniform: The diameter of each particle is randomly sampled at runtime from a uniform probability density function with a user-set minimum and maximum diameter.
Normal: The diameter of each particle is randomly sampled at runtime from a normal probability density function with a user-set mean and standard deviation.
Log Normal: The diameter of each particle is randomly sampled at runtime from a log-normal probability density function with a user-set log mean and log standard deviation.
Rayleigh: The diameter of each particle is randomly sampled at runtime from a Rayleigh probability density function with a user-set scale parameter.
Discrete Diameter Distribution: The diameter of each particle added to the system is randomly sampled at runtime from a user-specified particle diameter probability mass function.
Discrete Superquadric Distribution: A discrete superquadric (SQ) is a mathematical shape used to represent particles that are not perfectly spherical.
Discrete Volume Distribution: The diameter of each particle added to the system is randomly sampled at runtime from a user-specified particle volume probability mass function.
Initial Diameter UDF: This UDF defines the initial diameters of the particles entering the system.

`Forces and Fluid Coupling`¶

Discrete element particles are modeled as Lagrangian objects that move according to Newton’s second law. Within this framework, the time-evolution of the particle acceleration vector is linked to the sum of the external forces acting on the particle via the particle mass. The particle mass is calculated automatically from the instantaneous particle density and diameter.

Both unresolved and resolved DEM particle representations are available. Most CFD-DEM simulations use an unresolved particle representation. Unresolved particles are small compared to the lattice spacing, and the flow field around the particle is not explicitly resolved. As such, for unresolved particles, interactions (e.g., particle drag, lift) are modeled using empirical correlations. These interactions can be either one-way or two-way coupled to the fluid.

Resolved particles are large compared to the lattice spacing, meaning the flow field/boundary layer around the particle is resolved explicitly. Resolved models do not evoke any user-defined drag or lift coefficient; rather, since the flow is resolved, these forces are computed directly from the fluid field surrounding the particle. The fluid/particle forces are automatically two-way coupled. Resolved DEM simulations are an advanced modeling technique which typically require a large simulation resolution.

For both representations, custom forces and/or additional external forces can be defined via a UDF. For more discussion of these fluid particle forces, see the additional forces and fluid coupling overview.

Representation

This option specifies how the particles will be represented in the system.

Unresolved: Particles are assumed to be small compared to the lattice spacing. Fluid forces are calculated from user-set drag/lift relationships.
Resolved: Particles are assumed to be large compared to the grid spacing. Fluid forces are calculated directly from the flow field.

../../../_images/resolved-unresolved.png

The following graph indicates when to use resolved versus unresolved particles.

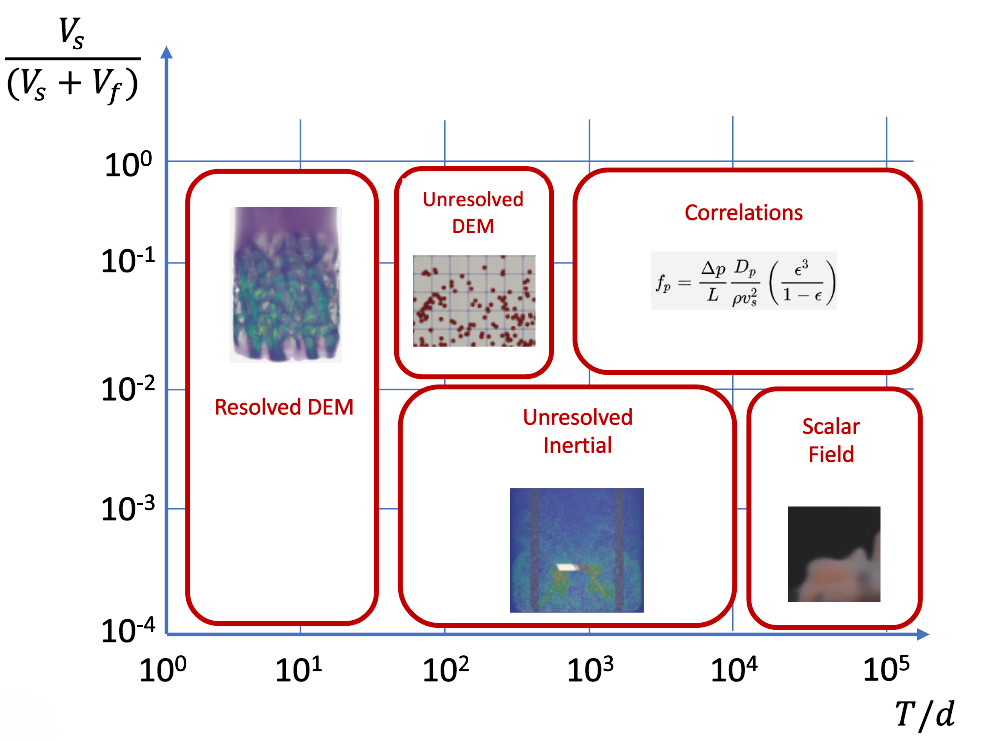
../../../_images/resolved-vs-unresolved.png

If Unresolved Particles are selected, the following options will appear:

See additional forces and fluid coupling overview.

Gravity/Buoyancy Force: This force represents the net effect of gravity and buoyancy.
Virtual Mass: The virtual mass refers to the virtual increase in the effective mass of a particle moving through fluid due to the inertia of the surrounding fluid.
Lift (Saffman): The Saffman lift force arises when a particle experiences a cross-flow induced by the rotation of the particle.
Drag Force Model: The drag force is the resistance encountered by particles as they move through the fluid medium.
Two Way Coupling: Two-way coupling describes the mutual interaction between fluid flow and particle motion.
Fluid-Particle Force UDF: This UDF defines custom vectors for fluid and external forces acting on particles.

Note

Interfacial transfer and scalar coupling are not currently supported for resolved particles.

Important

The high stiffness associated with solid particles means that CFD-DEM simulation typically requires a smaller solution timestep than CFD simulations without DEM particles. In general, small and stiff particles (e.g., higher Young’s modulus) require smaller solution timesteps than larger and less stiff particles. If the selected timestep is too large—meaning the particle dynamics are not stable—the simulation will lose particles over the course of the simulation. The code will report this behavior. This issue can be typically be resolved by either (1) decreasing the particle Young’s Modulus, (2) increasing the particle size, or (3) decreasing the simulation timestep. See the Choosing a DEM Timestep guide for more discussion.

If a static body is present, the following section will launch:

`Static Body Interaction`¶

This parameter specifies how each particle set interacts with each solid body family. When bounce interactions are specifed, the contact force is calculated using a Hertz contact model. Pass through and stick boundary conditions can also be specified.

Static Body Option

This parameter specifies how each particle set interacts with each solid body family.

Bounce Simple

Particle-solid interactions are calculated using the Hertz contact model. The properties of the solid wall, as used to calculate overlap and stiffness, are assumed to be:

Static Body Poisson Ratio: 0.3
Static Body Young’s Modulus: GPa | 0.1
Static Body Wall Coefficient of Restitution: 0.1
Static Body Wall Sliding Friction Coefficient: 0.5

Bounce Custom

Particle-solid interactions are calculated using the Hertz contact model. The properties of the solid wall, as used to calculate overlap and stiffness, are defined by the user. Default values are the properties evoked when using the Bounce Simple interaction option.

Static Body Poisson Ratio: 0.3
Static Body Young’s Modulus: GPa | 0.1
Static Body Wall Coefficient of Restitution: 0.1
Static Body Wall Sliding Friction Coefficient: 0.5

Stick

The particles stick to the solid surface. No physical properties are specified, and the particles remain stuck to the surface through the simulation. The motion control option, combined with an appropriate set of custom particle variations, should be used if more sophisticated stick and/or stick/release conditions are required.

Pass Thru

The particles do not interact directly with the solid body family.

`Particle-Particle Interaction`¶

These parameters define how particles interact with other particles. This section is only presented for Discrete Element and Resolved Particle types. See additional DEM particle overview.

Interaction Type

Type of inter-particle collisions.

Hertz Contact

Hertz contact model with user-defined particle properties listed below.

Young’s Modulus

GPa | Young’s modulus characterizes the tensile/compressive stiffness of the material. It is defined as the ratio of the stress (force per unit area) applied to the resulting axial strain. Typical values range from \(10^{-4}–10^3\) GPa. As discussed above, increasing the Young’s modulus will decrease the simulation timestep required to keep the contact mechanics stable.

Poisson’s Ratio

Poisson’s ratio characterizes the deformation of a material in directions perpendicular to the direction of loading. Typical values range from 0.2–0.3.

Coefficient of Restitution

The coefficient of restitution is the ratio of the relative velocity of separation after a collision to the relative velocity of approach before a collision. It can range from 0 (for a perfectly inelastic collision) to 1 (for a perfectly elastic collision).

Sliding Friction Coefficient

This coefficient is the ratio of the force of friction between two particles and the force pressing them together. Typical values of the friction coefficient range from 0.2–0.8.

Track Rotation

When this option is enabled, the torque, angular acceleration, and angular velocity of the DEM particles will be considered (in addition to the linear forces, translational acceleration, and linear velocities). These physics are particularly important for simulations with advanced contact mechanics involving irregularly shaped particles.

Off

Do not consider particle rotation.

On

Consider particle rotation.

Rolling Friction Coefficient: This coefficient represents the ratio of the rolling resistance to the normal/contact force. This coefficient typically ranges from \(10^{-3}–10^{-4}\).

Custom

A user-defined pairwise contact model. This expression defines the force vector on each particle as a function of interactions with nearby particles. This expression can be a function of particle properties (i.e., overlap distance, velocity, acceleration, diameter, and custom variables), and local fluid properties. Importantly, the force will only be active if there is a finite overlap force between the particles.

Interaction Cutoff

m | Particles with a separation distance greater than this cutoff will not be considered in any pair-wise interactions.

Inter-Particle Force UDF

N | This UDF defines the three components of a custom interaction force vector between two colliding DEM particles. Three outputs must be defined within the UDF: floating point variables name fx, fy, and fz. These output variables describe the x-, y-, and z-components of a custom interaction force vector between two colliding DEM particles.

In addition to the local fluid properties, the UDF input includes the properties (position, velocity, diameter, etc.) of both particles participating in the contact event as input values for evaluating the contact force UDF. In most cases, the line-of-action of the force vector will align with the particle-particle separation vector. Both particles participating in the reaction will experience the same force magnitude, although opposite in directions. This is a particle-based local UDF, calculated on a particle-by-particle basis using the local particle/fluid properties.

Download Sample File: Inter-Particle Force

Breakup/Coalesce ¶

Particle breakup and coalescence can be modeled using either discrete or parcel-based representations.

In the discrete representation, particle breakup occurs on a particle-by-particle basis and generates a new particle that is explicitly tracked in the simulation; this new particle inherits the properties of the mother particle from which it was broken off. Particle coalescence is regulated at the level of individual particle pairs by comparing the approach Reynold’s number to a critical coalescence parameter. Coalescence events reduce the number of explicitly tracked bubbles.

In the parcel-based representation, both particle breakup and coalescence are regulated implicitly by adjusting the number scale associated with each parcel. Changes in diameter are informed by the local fluid properties which, when combined with surface tension and density, define an equilibrium particle diameter. With this approach, the number of explicitly tracked particles does not change due to breakup or coalescence events. See additional breakup/coalesce overview.

Breakup Enabled: Particle breakup typically occurs on the level of individual particles. It is informed by the physical properties of the particle and the kinematic properties of the fluid.
Coalesce Enabled: Coalescence typically occurs at the level of particle pairs. It is informed by the kinematic properties of the two particles.

`Interfacial Mass Transfer`¶

Interfacial mass transfer is calculated on a particle-by-particle basis using the local and instantaneous fluid and particle properties. This can be represented as either a convective transfer coefficient, \(k_L\), or a particle dissolution rate. In principle, the convective transfer coefficient and the dissolution rate describe very similar physical transport processes. In practice, a convective transfer coefficient is typically applied to gas bubbles and a dissolution rate is applied to solid particles.

../../../_images/particle-dissolution.gif

Mechanically speaking, the convective transfer coefficient describes the rate at which mass is transferred (via convection) through the fluid boundary layer surrounding the particle. This rate is often written in terms of the local fluid energy dissipation rate, fluid viscosity, and fluid diffusion coefficient; although, in many cases a constant transfer coefficient may be suitable.

Theoretically speaking, most convective mass transfer models are developed under the assumption that the fluid immediately surrounding the particle remains fully saturated throughout the transport process. The rate at which mass is transferred into the system is therefore a function of the rate at which the saturated fluid adjacent to the bubble surface can be engulfed into the fluid bulk. These transfer functions can be derived from semi-empirical boundary layer theory.

Conversely, particle dissolution rates are developed under the assumption that the dissolved species concentration is low relative to the solid phase concentration. As such, the transfer rate is often related to the system temperature and the physiochemical properties of the solid rather than to the convective properties of the fluid surrounding the solid. In many cases, the dissolution rate is set to a constant value determined empirically.

Framework

This parameter determines whether mass transfer is modeled using the convective transfer coefficient or the particle dissolution rate. These values are calculated on a particle-by-particle basis using the local and instantaneous particle and/or fluid properties.

Convection

This calculates a convective mass transfer coefficient for each particle. Input to this expression includes the local and instantaneous properties of the particle and surrounding fluid.

kL UDF

m/s | This UDF defines the convective mass transfer coefficient in the fluid surrounding a particle. One output must be defined within the UDF: a floating-point variable named kl_{Particles}, where {Particles} is the dynamic name of the particle set. This output value is used when predicting convective mass transfer processes, including mass exchange with coupled scalar fields. This is a particle-based local UDF, calculated on a particle-by-particle basis using the local particle/fluid properties.

Download Sample File: kL

Dissolution

This calculates a dissolution rate for each particle. Possible input to this expression includes the local and instantaneous properties of the particle and surrounding fluid.

Dissolution Rate UDF

\(\frac{kg}{m^2 \cdot s}\) | This UDF defines the particle dissolution rate, defined here as the rate at which mass is exchanged between the solid phase (particles) and the dissolved phase/solute (coupled scalar field). One output must be defined as within the UDF: a floating point variable named dr_{Particle Set Name}, where {Particle Set Name} is the dynamic name of the particle set parent.

This output value defines the particle-specific dissolution rate. Positive values imply dissolution (mass leaving the particle). Negative values imply precipitation or crystallization. The units on the output variable are kg/m ² /s. This is a particle-based local UDF, calculated on a particle-by-particle basis using the local particle/fluid properties.

Download Sample File: Dissolution Rate

None

No mass transfer coefficient or dissolution rate is calculated.

If Interfacial Mass Transfer is on and a scalar is added, the following section will launch:

`Scalar Coupling`¶

Coupling Method

This option determines if particle-fluid scalar coupling is active in the simulation and whether it is modeled using built-in or user-defined functions. See additional scalar coupling overview.

Automatic: Predefined convection and/or dissolution models determine scalar transport rate, calculated on a particle-by-particle basis. The units on these properties depend on system setup and must be dimensionally homogeneous. Transport by convection is calculated from the user-specified convective transfer coefficient, the particle surface area, and the differences between the local concentration and the saturation limit. Transport by dissolution is calculated using the dissolution rate and the particle surface area. The same transport model is applied to all species participating in interfacial mass transfer.
Custom: User-defined transport models determine scalar transport rate, calculated on a particle-by-particle basis. These models could include the user-defined convective transfer coefficient, the user-defined dissolution rate, particle custom variables, or arbitrary functions of the local fluid/properties. A unique transport model can be specified for each species. The user must confirm that the transport parameters are dimensionally homogeneous.
None: No particle-fluid scalar coupling is considered. Although a convective transfer coefficient or dissolution rate may be defined, no species will be transferred between the particles and fluid.

`Thermal Coupling`¶

Track Temperature

This option determines if particle temperature is tracked during the simulation. Temperature changes can be caused by either (i) endothermic/exothermic intra-particle reactions, (ii) convective heat exchange with the surrounding fluid, and (iii) particle-particle conduction between DEM particles. This function can be turned off or on.

Initial Temperature

K | This parameter defines the initial temperature of the particles in the set.

Heat Capacity

J/m ³ K | This parameter defines the heat capacity of the particles. The heat capacity informs how changes in the thermal energy affect changes in temperature.

Particle-Particle Conduction

This function considers particle-particle conductive heat transfer between DEM particles. This is useful when modeling heat conduction through a fixed bed of DEM particles.

Off

Does not calculate particle-particle conductive heat transfer.

On

Calculates particle-particle conductive heat transfer.

Conductivity: W/mK | Thermal conductivity of the particles. This parameter is used to link temperature difference to heat flux.
Youngs Modulus: GPa | Effective Young’s Modulus of the particle pair. This value is used to evaluate the contact area available for conduction.

Fluid Particle Heat Transfer Coupling Method

This option specifies whether energy will exchange with the surrounding fluid via interfacial heat transfer.

None: No particle-fluid heat transfer is considered. The particle temperature will change only due to either endothermic/exothermic intra-particle reactions or particle-particle conduction between DEM particles.
Convection: Predefined convection model determines heat transport rate, calculated on a particle-by-particle basis. The functional form of the heat transfer model is discussed in the particle heat transfer overview.

UDF

The user defines a custom fluid-particle heat transfer rate.

Heat Transfer UDF

W | This UDF defines the heat transfer between particles and the surrounding fluid. One output must be defined within the UDF: a floating-point variable named Qdot. This output variable defines heat flow between the particle and the surrounding fluid. Positive values imply heat transfer into the particle (from the surrounding fluid). Negative values imply heat transfer away from the particle (into the surrounding fluid). The functional form of the heat transfer model is discussed in the particle heat transfer overview. This is a particle-based local UDF, calculated on a particle-by-particle basis using the local particle/fluid properties.

Download Sample File: Heat Flux

`Advanced`¶

Injection Downsampling

This parameter reduces the number of particles added to the system relative to the user-specified dump value, feed rate, initial volume fraction, initial mass fraction, or initial mass. Specifying a downsampling value transforms the particles into sampling parcels. These parcels are characterized by a parcel number scale and parcel diameter. The number scale quantifies the number of equal-sized particles contained within each parcel. The parcel diameter is equal to the particle diameter, as defined by the size distribution. To ensure that the mass represented by the parcels equals the user-specified dump or feed rate, all parcels entering the system are assigned an initial number scale equal to this injection downsampling parameter. The amplifying effects of the number scale on all particle-to-fluid forces, local particle volume fraction calculations, and interfacial mass transfer rates are handled internally and automatically.

With injection downsampling, not all particles are represented explicitly, so systems with injection downsampling are typically paired with the parcel-based breakup and coalescence representation. Thus the model underpredicts pair-wise collisions and explicit coalescence events.

The purpose of the downsampling is to reduce the memory requirements of a simulation. Increasing the number scale (the number of equal-sized particles contained within each parcel) will have the effect of reducing the number of explicitly tracked parcels in the system. The downsampling number should be kept as small as possible, which can minimize the effects of improper course graining and undersampling. In practice, we recommend keeping the number of parcels within the system order-of-magnitude consistent with the lattice count.

This parcel-based representation is also applied to the parcel-based breakup and coalescence representation and discussed in our webinars and reference literature.

For systems with either the Hertz Simple or Hertz Contact model, the effective collision diameter of the particles will increase as the cube root of the initial number scale. This scaling ensures that the volume occupied by the particles/packed bed matches expectations.

In the video below, we illustrate the effects of injection downsampling on particle filling for a simple DEM system. Both cylinders are filled with 1 mm diameter particles. This diameter informs the particle trajectory during free-fall, which is similar in both systems.

When the injection downsampling is set to 1, as shown on the left, 300,000 individual particles are added to the system. The resulting packed bed is approximately 5 cm deep. When the injection downsampling is set to 2, as shown on the right, only 150,000 individual particles are added to the system. The resulting packed bed height is still 5 cm, however, due to the increased effective particle collision diameter imposed as part of the downsampling.

Both systems have similar free-fall dynamics (when the distances between particles are large). Moreover, both systems have a similar final/equilibrium packed-bed shape (where the particles are in constant contact). The downsampled system, however, requires two times less memory to produce similar results.

The injection number scale is numerical convenience introduced to make simulations more computationally tractable. As with other parcel methods, the sensitivity of the simulation predictions to the injection number scale should be considered as part of a grid convergence study.

Download Sample File: Number Scale DEM

DEM Bounce Method

This options for this method defines how the particles interact with solid bodies. The video below shows the difference between the two options.

Cell: This is the default option. It is computationally faster than Triangle method. The particles interact with the boundaries of the fluid voxels. Smaller particles, can get caught on the “steps” for coarser resolutions. As the lattice resolution increase, this effect is minimized.
Triangle: In this option, the particles interact with the triangles made from the tessellation of the static body surface. This is more computationally expensive than the Cell option, but results in a more physically realistic interaction with the static body. The size of the triangles used to represent the surface is set using the edit mesh form. The corresponding mesh can be previewed using the Preview Surface Meshes tool.

Initial Velocity Type

By default, particles enter the system with zero velocity. Users may override this setting by assigning the particles a non-zero velocity. This velocity can be specified as either a constant value or a user-defined function of local fluid properties, particle properties, system variables, etc.

Constant

Under this option, all particles in the family entering the system will have the initial velocity defined below. By default, this value is set to a zero vector, implying no initial velocity.

Initial Velocity: m/s | This is the initial translational velocity vector of the particles entering the system. The three fields define the x, y, and z components of the velocity vector. These vectors are aligned with the basis x, y, and z unit vectors within the system.

Custom UDF

Under this option, all particles in the family entering the system will have an initial velocity computed at runtime from the UDF.

Initial Velocity UDF

m/s | The UDF defines the initial velocity of particles as they are added to the system. Three outputs must be defined within the UDF: floating point variables vx_p, vy_p, and vz_p. These output variables define the components of the initial velocity vector of the particles entering the system. This is a particle-based local UDF, calculated on a particle-by-particle basis using the local particle/fluid properties.

Download Sample File: Initial Velocity

Note

For injections at inlet boundary conditions, the initial particle velocity may be set to the inlet velocity to model a set of pre-entrained particles.

Compute Nearest Neighbor Distribution

Computes the average nearest neighbor separation distance and nearest neighbor separation distance probability distribution function. See additional discussion in Theory: Nearest Neighbor Distribution.

On: Particle distribution data is computed.
Off: Particle distribution data is not computed.

Enable Particle Freezing

With this option, users can specify a time at which a particle set becomes fixed in space. Once frozen, all particle dynamics and any particle-particle interactions are disabled. This feature is particularly useful for creating packed bads using DEM particles and then flowing flow through the interstitial gaps. Electing to freeze the particles can improve simulation efficiency as the code no longer runs the particle-particle contact wall interaction, and position integration kernels. Once frozen, dynamics cannot be reactivated. All other updates, including scalar coupling and thermal transport, will still be considered.

On

Enable particle freezing.

Start Time: Time at which to being particle freezing.

Off

Do not consider particle freezing.

Enable Movement Control

With this option, users can define a UDF that conditionally controls whether particles are moving or fixed. Particle motion can be reactivated as part of the UDF. Control is specified on a particle-by-particle basis. This functionality only prevents updates to the particle position/velocity. All other particle physics—including particle-particle interactions, particle-scalar coupling, etc.—continue as defined.

On

Movement control of particles is enabled. Individual particles may become fixed in space per some user-defined condition.

Movement Control UDF

none | This UDF defines if individual particles move or remain fixed in space. One of two possible boolean outputs can be defined as part of the UDF: makeFixed and makeMoving. The values assigned to each value can change over time. If the boolean makeMoving is set to true, the particle will evolve through space. Only one boolean should be true at each time step. This is a local UDF, calculated on a particle-by-particle basis using the local particle/fluid properties.

Download Sample File: Movement Contol

Off

No controlled movement of particles. Particles always have the ability to move through space.

Compute Pressure Gradient Force

When this option is active, the pressure gradient force on the particle is calculated. This force acts from regions of higher pressure toward regions of lower pressure, influencing the motion of particles immersed in the fluid.

For a small particle within a fluid, the pressure gradient force can be expressed as:

\[F_p = - V_p \nabla P\]

where \(V_p\) is the volume of the particle and \(\nabla P\) is the pressure gradient and the location of the particle.

Off: Does not compute pressure gradient force.
On: Computes pressure gradient force.

Enable Removal UDF

Enable removal user-defined function.

Removal UDF

no units | This UDF removes particles based on particle properties or local fluid conditions. One output must defined within the UDF: a Boolean variable named remove. This output value determines if a particle is to be removed from the simulation. If set to true, the particle is removed. This is a local UDF, calculated on a particle-by-particle basis using the local particle/fluid properties.

Download Sample File: Removal