 Single Phase¶
Single Phase¶
Introduction¶
Single phase configurations are simulations involving a single base fluid with Newtonian or non-Newtonian rheology and no interface. This is the most common fluid configuration. Fluid mechanics are modeled explicitly via the Navier-Stokes equations. Within this configuration, users must specify the fluid density and define the constitutive relationship between fluid stress and fluid strain. Common applications include pipe flow simulations, well-baffled agitated tanks, jet mixing systems, and pumps.
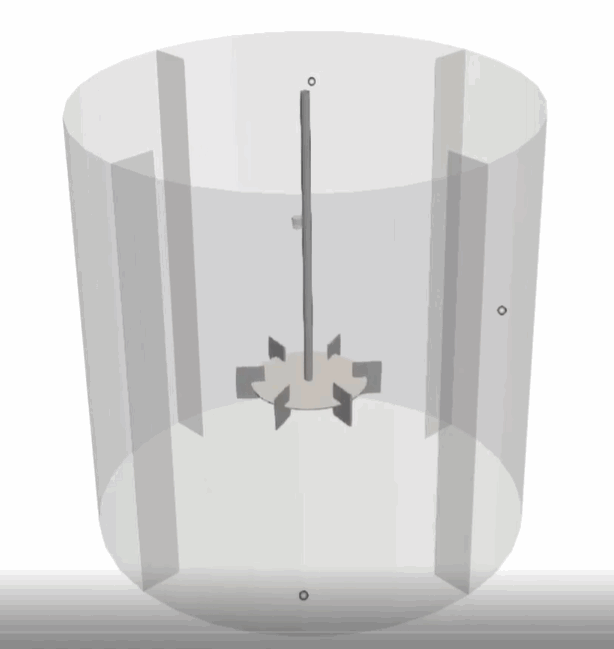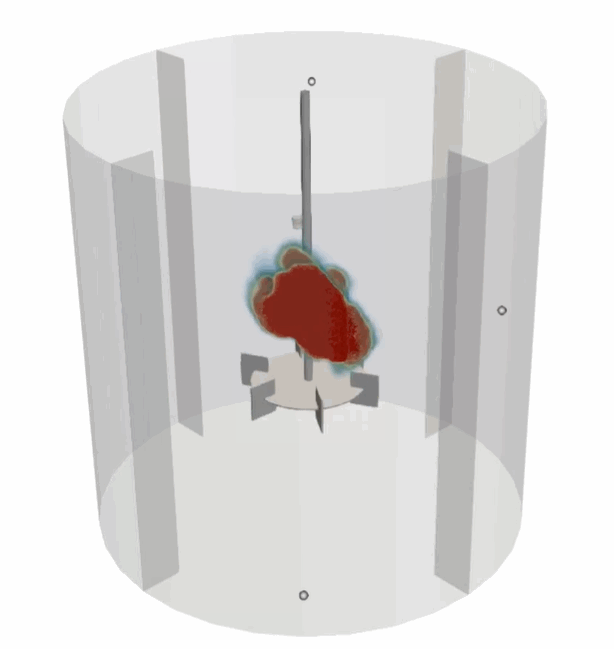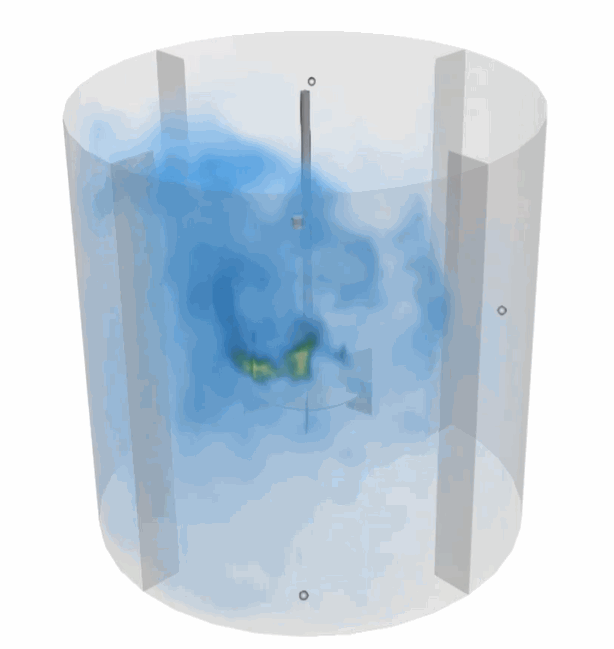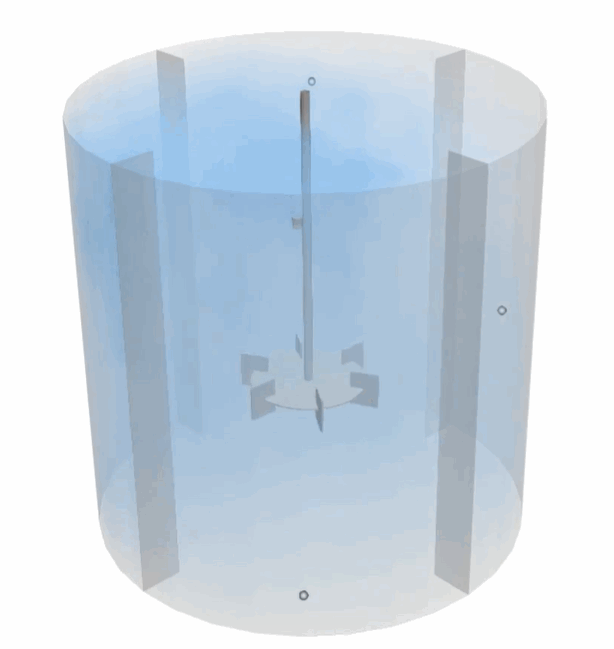
As discussed in particleFields, additional phases (such as discrete bubbles and discrete solid particles) can be added to the system and one- or two-way coupled to the fluid. Secondary miscible fluids with arbitrary densities and viscosities, as discussed in Miscible Scalar, can be also added to the base fluid. Additionally, thermal fields and scalar fields can be superimposed on the single phase fluid, as discussed in Thermal and fluidscalar.
The context-specific Single Phase Toolbar offers a help link to relevant documentation.
Property Grid¶
Fluid Properties¶
The single phase property grid is customized based on your fluid properties. Select the rheology type from the tabs below to show the accompanying grid.
- Rheology Type
- Newtonian
A fluid with a constant and uniform viscosity.
- Power-law
Local fluid viscosity is calculated from the local shear rate using a user-defined flow consistency index, flow behavior index, and yield stress.
- Carreau
Local fluid viscosity is calculated from the local shear rate using a user-defined characteristic time, power index, and infinite/zero share rate viscosities.
- Cross
Local fluid viscosity is calculated from the local shear rate using a user-defined rate constant, time constant, and infinite/zero share rate viscosities.
- Bingham Plastic
A viscoelastic fluid with a user-defined yield-stress and viscosity.
- Custom Fluid
A user-defined expression for the local fluid viscosity.
Configuration¶
These properties define the configuration of the fluid, including the turbulence type and any external acceleration.
- Initial Fluid Pressure
Pa | Initial pressure of the fluid inside the system.
- Turbulence Model Type
Fluid turbulence model to be applied to the simulation.
- DNS
Direct Numerical Simulations (DNS) attempt to resolve all fluid motion across all eddy scales. If the smallest eddies approach the lattice spacing, the simulation becomes unstable and may diverge.
- Lattice Type
This setting defines the number of discrete microscopic velocity vectors considered at each lattice point. The D3Q19 and D3Q27 lattice models differ primarily in the number of discrete velocity directions. The D3Q19 model has 19 possible velocity directions, while the D3Q27 model has 27. The additional directions in the D3Q27 lattice allow it to capture more complex flow details, particularly in simulations involving higher Reynolds numbers or intricate boundary interactions.
However, this increased complexity comes at a cost: the D3Q27 model typically requires about 40% more memory and runs about 40% slower than the D3Q19 model, making it more computationally demanding. When choosing between them, consider the trade-off between accuracy and computational efficiency. D3Q27 may be preferred for simulations which require high precision in flow characteristics, whereas D3Q19 may be preferable when the priority is computational efficiency.
- D3Q19
Uses a D3Q19 lattice.
- D3Q27
Uses a D3Q27 lattice.
- LES
Large Eddy Simulation (LES) models resolve the largest, energy-containing turbulent motions directly while modeling the smaller, subgrid-scale (SGS) turbulence through a computed eddy viscosity based on the local shear rate. This eddy viscosity is added to the molecular viscosity when solving the Navier-Stokes equations. LES models are generally stable across a wide range of Reynolds numbers. The influence of the filtering on the flow decreases as the resolution increases.
- Lattice Type
This setting defines the number of discrete microscopic velocity vectors considered at each lattice point. The D3Q19 and D3Q27 lattice models differ primarily in the number of discrete velocity directions. The D3Q19 model has 19 possible velocity directions, while the D3Q27 model has 27. The additional directions in the D3Q27 lattice allow it to capture more complex flow details, particularly in simulations involving higher Reynolds numbers or intricate boundary interactions.
However, this increased complexity comes at a cost: the D3Q27 model typically requires about 40% more memory and runs about 40% slower than the D3Q19 model, making it more computationally demanding. When choosing between them, consider the trade-off between accuracy and computational efficiency. D3Q27 may be preferred for simulations which require high precision in flow characteristics, whereas D3Q19 may be preferable when the priority is computational efficiency.
- D3Q19
Uses a D3Q19 lattice.
- D3Q27
Uses a D3Q27 lattice.
- Smagorinsky Coefficient
Only relevant for LES simulation. This value is set to 0.1, a value motivated by predictions from direct numerical simulation.
- ILES
Implicit Large Eddy Simulation (ILES) resolves the largest turbulent motions directly, like LES, but does not use an explicit SGS model. Instead, the numerical dissipation inherent in the discretization scheme provides stabilization and effectively models the small-scale turbulence.
The M-Star ILES turbulence model requires a D3Q27 lattice and is set automatically by the solver at runtime to maintain stability at high Reynolds numbers. This approach simplifies implementation and reduces parameter tuning compared with conventional LES.
Single Phase Toolbar¶
Context-Specific Toolbar Forms |
Description |
|---|---|
|
The Help command launches the M-Star reference documentation in your web browser. |
For a full description of each option, see Context-Specific Toolbar selections.
 Help
Help